北京五輪 女子カーリング どの統計量を使うかで予選の順位は変わった?

増川 直裕
- ■日本が予選を通過できた仕組み
- ■ドローショットチャレンジとは?
- ■LSDの分布と悪い結果を除くということ
- ■チームごとのLSDの分布と日本のパフォーマンスは
- ■他の統計量でも順位をつけてみると
- ■日本が予選3位であったならば
■日本が予選を通過できた仕組み
北京五輪では、最初から最後まで日本女子カーリングの話題が事欠かなかったですね。お互いのチームが火花をぶつけあう予選リーグで日本は苦戦をし、イギリス、カナダと並ぶ5勝4敗でしたが、勝敗が並んだ時の順位の決め方であるドローショットチャレンジ(DSC) でカナダより成績が上だったため、辛くも4位でギリギリ予選を通過しました。
筆者自身、にわかなカーリング視聴者のため、このようなルールで順位を決めることを知らなかったのですが、カーリングでは相手の勝ちを認めて試合を終了するコンシードという制度があるため、単純に得失点差では判断できないことが理由にあるようです。
本記事では、このドローショットチャレンジ(DSC) の結果を統計的に考えてみます。最初に、このルールを説明し、各チームのDSCの結果を見ていきます。
次に、このルールで使う統計量によっては、日本の予選順位が上がり、イギリスとの決勝戦で有利に戦うことができたのかも?といったことを述べていきます。
■ドローショットチャレンジとは?
カーリングでは、試合の最初に先攻、後攻を決めるために、各チームが2投ずつ行い、ハウスの中心からの距離を競うラストストーンドロー(LSD)を行います。その際、2投の平均距離が短い方が、先行、後攻を決めることができます。
今回の予選リーグは、各チーム9試合あったため、合計18回の距離データがあり、この中から距離が長い2つのデータを除き、16回の距離データの平均をとったものが、DSC(ドローショットチャレンジ)となります。
予選リーグで勝敗が並んだ場合は、このDSCの値が小さい順に順位が上位になるという仕組みになっています。
下に示す表では、予選リーグの順位(予選リーグ Rank)、DSCの順(DSC Rank)、DSCの値(平均)を示しています。
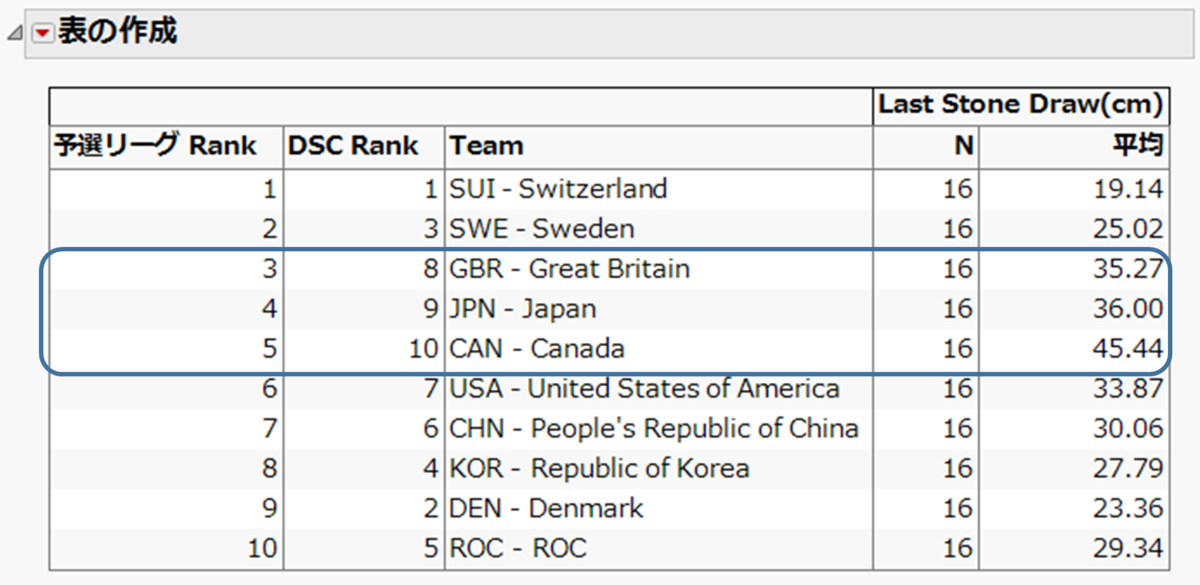
先に記載したように、予選リーグでは、イギリス、日本、カナダが5勝4敗で、勝敗では同一の結果だったのですが、DSCの値をみると、それぞれ35.27、36.00、45.44 であったため、イギリス3位、日本4位、カナダ5位となったのです。予選落ちしたカナダは、この決め方に不満のようですが。
DSCの値で順位をつけると、この3チームが8、9、10位と下位になっているのが興味深いところでもあります。
■LSDの分布と悪い結果を除くということ
ここで、全チームの予選におけるLSDの分布を調べてみます。各チーム18投で10チームあるので、180個のデータの分布になります。

筆者は、この分析をする前に、どこかの値を中心に対称っぽい分布になるのかなと思っていたのですが、そんなことは全くありませんでした。いわゆる右に長い裾を引いている分布になっているのです。
ヒストグラムをみると、多くは25cm以内に収まっているのですが、一方で100cmを超えているデータもいくつかあります。ちなみに、ハウスに入らなかったときの距離は、一律で199.6cmとして計測されるようなので、199.6という値のデータが3つほどあります。
確かにこのようなデータで単純に平均をとると、値が大きいデータに引っ張られて、平均が大きくなってしまいます。
先に記載したように、DSCの計算では、最も悪かった結果とその次に悪かった結果の2つを除いて平均をとっています。そのため、極端に悪い結果はDSCの計算からは除かれるので、悪すぎるパフォーマンスは、結果にあまり影響を及ぼさないといったことになります。
■チームごとのLSDの分布と日本のパフォーマンスは
次に、チームごとのLSDの分布を調べてみます。下図は、チームをDSCの成績が良い順に並べ、各国18回のLSDの値をプロットで示し、箱ひげ図も描いています。プロット点で赤色の点は、DSCの計算からは除かれたデータ(値が大きい上位2つ)です。
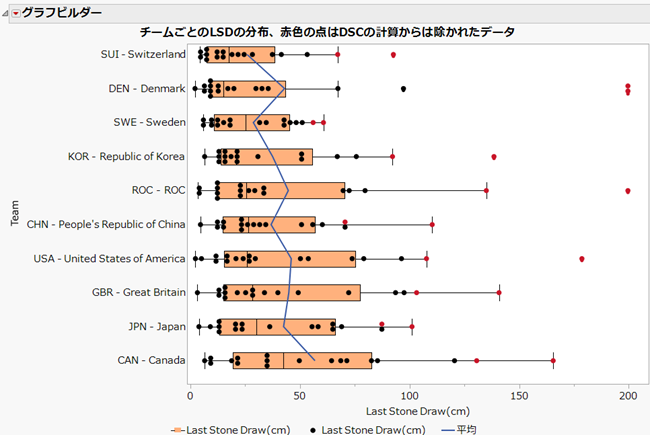
図の下側にイギリスと日本とカナダの分布が描かれていますが、日本の最大値は、他の2か国に比べてかなり小さいことがわかります。すなわち、大きく円から外れたショットが他の2か国に比べて、あまりなかったわけです。
この結果だけ考えれば、日本は優秀なように思えますが、DSCという方法は、値が極端に大きくても上2つのデータは除かれるがために、結果としてイギリスの方が良かったということになります。
スキージャンプなどの複数の人が採点する競技では、極端に大きく点をつける人や極端に悪く点をつける人の影響を除くために、例えば5人の採点者がいたら、最も良い点数と最も悪い点数を除いたものを評点として扱うといったことが良く行われています。
しかし、今回のカーリングは採点者の主観が混ざるわけではなく、円からの距離といった客観的な結果なので、悪い結果(円からかなり離れている)を出した方が悪いと考え、悪いデータは除かず、全体のデータで平均を求めるといったこともありなのかもしれません。
ちなみに、上の図には青色の折れ線が示されていますが、この線は、各チームの18回全体での平均値を結んだものです。すると、若干ではありますが、イギリスより日本の方が平均値は小さくなります。すなわち、全体の平均値でLSDのパフォーマンスを測ると、日本がイギリスより良くなるのです。
当然ながら勝手にルールは変えられませんが、悪い結果を除かないで単純に平均をとるルールであれば、日本が予選3位で、イギリスが予選4位だったわけです。
■他の統計量でも順位をつけてみると
ここまでで述べたDSC(値が大きい2つのデータを除いた平均)、(単純)平均値の他にも、中央値で検討する、第3四分位点である75%点で検討するといったこともやってみました。
下図は、これらの方法で求めたものを表としてまとめたものです。セルには色がついていますが、セルの値で順位をつけたとき、濃い色になるほど値が大きい、すなわち下位の順位になることを示しています。
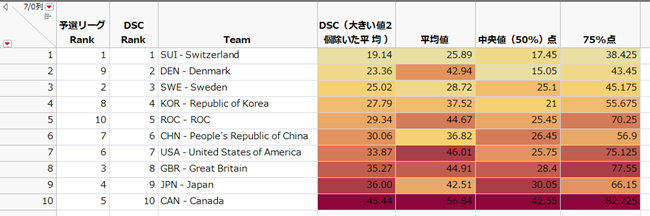
下から3番目のイギリスと2番目の日本を比べてみましょう。中央値では日本はイギリスに負けてしまいますが、75%点では、日本はイギリスに大きく差をつけて勝っています。使う統計量によっては、イギリスが良かったり、日本が良かったりするのです。
■日本が予選3位であったならば
ここまで読まれた方は、あまのじゃくな人が考えたネタだなと思っているかもしれません。ただ、スポーツ競技において、今回のような統計量として何を使うのかといったルールによっても、結果が変わってしまう可能性があるといった一つの例を示したわけです。
もし日本が予選3位でイギリスが予選4位であれば、イギリスと日本の決勝戦では、日本が予選の順位でイギリスを上回っているため、最初の第1エンドは、一般的に有利であるといわれる後攻をとることができました。(実際は、イギリスの方が上回っていたので、イギリスが後攻でした。)
もし、最初に後攻でスタートして良いパフォーマンスができていれば、決勝の結果も変わっていたかも……と考えるのでは少し強引すぎるでしょうか。
■ さあ始めよう!
JMPの全機能を30日間試せるトライアル版で、データからさらなる情報を導き出せることを実感してください。
さあ始めましょう。ダウンロードはコチラ!
■ JMPについて
JMP(ジャンプ)は世界中のエンジニア、データアナリストに選ばれているインタラクティブで可視的なデータ分析ツールです。
< SNSで様々な情報をお届けしています >